感觉大家都会同源,就我不会,花了两天的时间对着鸡块blog 和huangx607087 学习了一下
对于有限域 G F ( p r ) GF(p^r) G F ( p r ) E E E O O O 1 ≡ O m o d p 1\equiv O\mod p 1 ≡ O m o d p E E E
1 2 3 4 5 6 7 p = 283 E = EllipticCurve(GF(p ^ 2 , name="i" , modulus=[1 , 0 , 1 ]), [1 , 0 ]) print (E.order() % p == 1 , E.is_supersingular())E = EllipticCurve(GF(p ^ 2 , name="i" , modulus=[1 , 0 , 1 ]), [1 , 1 ]) print (E.order() % p == 1 , E.is_supersingular())
一般来说,超奇异椭圆曲线是在 G F ( p 2 ) GF(p^2) G F ( p 2 ) p % 4 = 3 p\%4=3 p % 4 = 3
对于有限域 G F ( p r ) GF(p^r) G F ( p r ) E : y 2 = x 3 + a x + b E:y^2=x^3+ax+b E : y 2 = x 3 + a x + b
j = 1728 ( 4 a ) 3 − Δ j=\frac{1728(4a)^3}{-\Delta}
j = − Δ 1 7 2 8 ( 4 a ) 3
其中 Δ = − 16 ( 4 a 3 + 27 b 2 ) \Delta=-16(4a^3+27b^2) Δ = − 1 6 ( 4 a 3 + 2 7 b 2 ) Δ = 0 \Delta=0 Δ = 0
1 2 3 4 5 6 7 8 9 10 from Crypto.Util.number import getPrimep = getPrime(256 ) a = getRandomRange(1 , p) b = getRandomRange(1 , p) E = EllipticCurve(GF(p), [a, b]) j1 = E.j_invariant() Δ = -16 * (4 * a ^ 3 + 27 * b ^ 2 ) j2 = 1728 * (4 * a) ^ 3 * inverse_mod(-Δ, p) % p assert j1 == j2
如果两条曲线的j-不变量相同,则两条曲线同构,即存在映射:
ϕ : E 1 ( x , y ) ↦ E 2 ( x ′ , y ′ ) \phi:E_1(x,y)\mapsto E_2(x',y')
ϕ : E 1 ( x , y ) ↦ E 2 ( x ′ , y ′ )
对于 G F ( 41805 1 2 ) GF(418051^2) G F ( 4 1 8 0 5 1 2 ) E 1 : y 2 = x 3 + x + 1 , E 2 : y 2 = x 3 + 146258 ∗ x + 405280 E_1:y^2 = x^3 + x + 1,E_2:y^2 = x^3 + 146258*x + 405280 E 1 : y 2 = x 3 + x + 1 , E 2 : y 2 = x 3 + 1 4 6 2 5 8 ∗ x + 4 0 5 2 8 0
ϕ : E 1 ( x , y ) ↦ E 2 ( − 122373 x , − 206462 y ) \phi:E_1(x,y)\mapsto E_2(-122373x,-206462y)
ϕ : E 1 ( x , y ) ↦ E 2 ( − 1 2 2 3 7 3 x , − 2 0 6 4 6 2 y )
可以使用sage计算
1 2 3 4 5 6 7 8 9 10 11 p = 418051 R.<i> = GF(p ^ 2 , name="i" , modulus=[1 , 0 , 1 ]) E1 = EllipticCurve(R, [1 , 1 ]) E2 = EllipticCurve(R, [146258 , 405280 ]) assert E1.j_invariant() == E2.j_invariant()assert E1.is_isomorphic(E2)phi = E1.isomorphism_to(E2) phi.rational_maps() G = E1.random_point() E2([-122373 *G[0 ], -206462 *G[1 ]])
而对于任意的p,其上面超奇异椭圆曲线j-不变量的个数为 ⌊ p 12 ⌋ + z \lfloor\frac{p}{12}\rfloor+z ⌊ 1 2 p ⌋ + z z z z
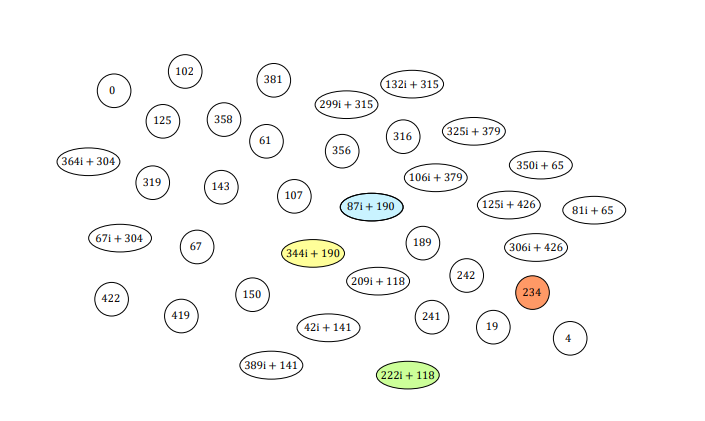
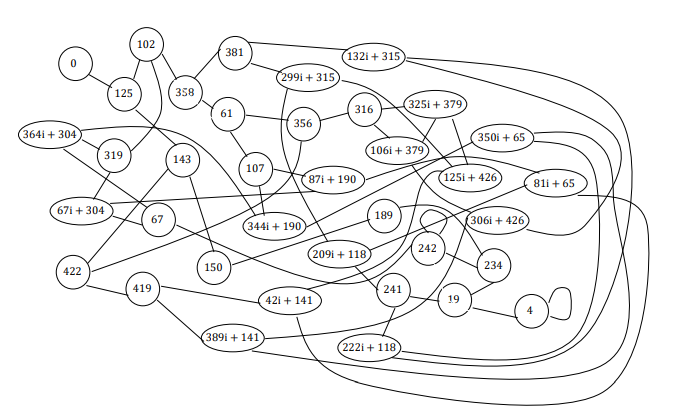
下图为当 p = 431 p=431 p = 4 3 1 G F ( p 2 ) GF(p^2) G F ( p 2 )
我们在ECC中常用的曲线形式一般都为 Short Weierstrass curves 即 y 2 = x 3 + a x + b y^2=x^3+ax+b y 2 = x 3 + a x + b Montgomery Curve 的形式为 y 2 = x 3 + A x 2 + x y^2=x^3+Ax^2+x y 2 = x 3 + A x 2 + x Short Weierstrass curves 都可以映射为 Montgomery Curve。
1 2 3 4 5 p = 418051 R.<i> = GF(p ^ 2 , name="i" , modulus=[1 , 0 , 1 ]) E1 = EllipticCurve(R, [1 , 1 ]) E1.montgomery_model()
对于 Montgomery Curve 而言其得j-不变量的计算方式为
j = 256 ( A 2 − 3 ) 3 A 2 − 4 j=\frac{256(A^2-3)^3}{A^2-4}
j = A 2 − 4 2 5 6 ( A 2 − 3 ) 3
相较于ECC点对点的运算,同源可以相当于两条曲线之前的映射关系,其实前面在里面也已经提到过了。举一个简单的例子,将一条曲线对自己的二倍点进行映射
1 2 3 4 5 6 p = 418051 R.<i> = GF(p ^ 2 , name="i" , modulus=[1 , 0 , 1 ]) E = EllipticCurve(R, [1 , 0 ]) phi = E.scalar_multiplication(2 ) print (phi.rational_maps())
可以得到映射为
ϕ : ( x , y ) ↦ ( x 4 − 2 x 2 + 1 4 x 3 + 4 x , x 6 y + 5 x 4 y − 5 x 2 y − y 8 x 6 + 16 x 4 + 8 x 2 ) \phi:(x,y)\mapsto \left(\frac{x^{4} - 2 x^{2} + 1}{4 x^{3} + 4 x}, \frac{x^{6} y + 5 x^{4} y - 5 x^{2} y - y}{8 x^{6} + 16 x^{4} + 8 x^{2}}\right)
ϕ : ( x , y ) ↦ ( 4 x 3 + 4 x x 4 − 2 x 2 + 1 , 8 x 6 + 1 6 x 4 + 8 x 2 x 6 y + 5 x 4 y − 5 x 2 y − y )
当然,我们可以令 4 x 3 + 4 x = 0 4 x^{3} + 4 x=0 4 x 3 + 4 x = 0 [ 0 , i , − i ] [0,i,-i] [ 0 , i , − i ] division_points
1 2 E(0 ).division_points(2 )
同样的,其也可以对自己的四倍点进行映射
1 2 3 phi = E.scalar_multiplication(2) print(phi.rational_maps()) E(0).division_points(4)
可以得到
ϕ : ( x , y ) ↦ ( x 16 − 40 x 14 + 348 x 12 + 1000 x 10 + 1478 x 8 + 1000 x 6 + 348 x 4 − 40 x 2 + 1 16 x 15 + 176 x 13 + 400 x 11 − 592 x 9 − 592 x 7 + 400 x 5 + 176 x 3 + 16 x , 32 x 24 y + 2176 x 22 y − 54208 x 20 y − 104832 x 18 y + 208870 x 16 y + 62991 x 14 y + 160405 x 12 y + 62991 x 10 y + 208870 x 8 y − 104832 x 6 y − 54208 x 4 y + 2176 x 2 y + 32 y 2048 x 24 + 34816 x 22 + 186368 x 20 − 198915 x 18 + 168454 x 16 + 102918 x 14 − 102918 x 12 − 168454 x 10 + 198915 x 8 − 186368 x 6 − 34816 x 4 − 2048 x 2 ) \phi:(x,y)\mapsto \left(\frac{x^{16} - 40 x^{14} + 348 x^{12} + 1000 x^{10} + 1478 x^{8} + 1000 x^{6} + 348 x^{4} - 40 x^{2} + 1}{16 x^{15} + 176 x^{13} + 400 x^{11} - 592 x^{9} - 592 x^{7} + 400 x^{5} + 176 x^{3} + 16 x}, \frac{32 x^{24} y + 2176 x^{22} y - 54208 x^{20} y - 104832 x^{18} y + 208870 x^{16} y + 62991 x^{14} y + 160405 x^{12} y + 62991 x^{10} y + 208870 x^{8} y - 104832 x^{6} y - 54208 x^{4} y + 2176 x^{2} y + 32 y}{2048 x^{24} + 34816 x^{22} + 186368 x^{20} - 198915 x^{18} + 168454 x^{16} + 102918 x^{14} - 102918 x^{12} - 168454 x^{10} + 198915 x^{8} - 186368 x^{6} - 34816 x^{4} - 2048 x^{2}}\right)
ϕ : ( x , y ) ↦ ( 1 6 x 1 5 + 1 7 6 x 1 3 + 4 0 0 x 1 1 − 5 9 2 x 9 − 5 9 2 x 7 + 4 0 0 x 5 + 1 7 6 x 3 + 1 6 x x 1 6 − 4 0 x 1 4 + 3 4 8 x 1 2 + 1 0 0 0 x 1 0 + 1 4 7 8 x 8 + 1 0 0 0 x 6 + 3 4 8 x 4 − 4 0 x 2 + 1 , 2 0 4 8 x 2 4 + 3 4 8 1 6 x 2 2 + 1 8 6 3 6 8 x 2 0 − 1 9 8 9 1 5 x 1 8 + 1 6 8 4 5 4 x 1 6 + 1 0 2 9 1 8 x 1 4 − 1 0 2 9 1 8 x 1 2 − 1 6 8 4 5 4 x 1 0 + 1 9 8 9 1 5 x 8 − 1 8 6 3 6 8 x 6 − 3 4 8 1 6 x 4 − 2 0 4 8 x 2 3 2 x 2 4 y + 2 1 7 6 x 2 2 y − 5 4 2 0 8 x 2 0 y − 1 0 4 8 3 2 x 1 8 y + 2 0 8 8 7 0 x 1 6 y + 6 2 9 9 1 x 1 4 y + 1 6 0 4 0 5 x 1 2 y + 6 2 9 9 1 x 1 0 y + 2 0 8 8 7 0 x 8 y − 1 0 4 8 3 2 x 6 y − 5 4 2 0 8 x 4 y + 2 1 7 6 x 2 y + 3 2 y )
总的来说,对于阶为 l l l l l l
因此一个可分的同源可以描述为:对于曲线E和其的一个子群 G G G G G G ϕ : E 1 ( x , y ) ↦ E 2 ( x ′ , y ′ ) \phi:E_1(x,y)\mapsto E_2(x',y') ϕ : E 1 ( x , y ) ↦ E 2 ( x ′ , y ′ ) E 2 E_2 E 2
当然,在sage上同源有很好的实现
我们选择 ( 350 i + 68 , 0 ) (350i + 68,0) ( 3 5 0 i + 6 8 , 0 )
1 2 3 4 5 6 7 8 9 p = 431 R.<i> = GF(p ^ 2 , name="i" , modulus=[1 , 0 , 1 ]) E = EllipticCurve(R, [0 , 161 +208 *i, 0 , 1 , 0 ]) G = E(350 *i + 68 ,0 ) phi = E.isogeny(G) phi.codomain() phi.rational_maps()
我们可以注意到同源得到的曲线的j-不变量和原曲线不同,所以同源并不是同构,而同构可以算是同源的一种特殊情况。
一条曲线一个子群只能唯一对应一个同源
同源是同态的,即有 ϕ ( P + Q ) = ϕ ( P ) + ϕ ( Q ) \phi(P+Q)=\phi(P)+\phi(Q) ϕ ( P + Q ) = ϕ ( P ) + ϕ ( Q )
同源是对偶的
可以发现我们选择的 ( 350 i + 68 , 0 ) (350i + 68,0) ( 3 5 0 i + 6 8 , 0 ) 2 2 2
364 i + 304 ↦ 344 i + 190 364i + 304\mapsto 344i + 190
3 6 4 i + 3 0 4 ↦ 3 4 4 i + 1 9 0
而在 2 2 2
364 i + 304 ↦ 67 364 i + 304 ↦ 319 364i + 304\mapsto 67\\
364i + 304\mapsto 319
3 6 4 i + 3 0 4 ↦ 6 7 3 6 4 i + 3 0 4 ↦ 3 1 9
而如果我们以E的j-不变量为起点,将映射得到的曲线的j-不变量视为终点。然后持续这么做把所有点的 2 2 2 2 2 2
而同源是对偶的,所以同源图图也是无向图。
https://math.mit.edu/~drew/ClassicalModPolys.html
首先要选取类似如下形式的质数p
p = 2 e a 3 e b − 1 p=2^{e_a}3^{e_b}-1
p = 2 e a 3 e b − 1
然后在其二次扩域下定义曲线 E 0 : y 2 = x 3 + a x 2 + x E_0:y^2=x^3+ax^2+x E 0 : y 2 = x 3 + a x 2 + x
Alice在 E 0 E_0 E 0 2 e a 2^{e_a} 2 e a ( P 2 , Q 2 ) (P_2,Q_2) ( P 2 , Q 2 ) E 0 E_0 E 0 3 e b 3^{e_b} 3 e b ( P 3 , Q 3 ) (P_3,Q_3) ( P 3 , Q 3 ) E 0 E_0 E 0
只后Alice和Bob要分别选择自己的私钥 s A , s B s_A,s_B s A , s B
对于公钥生成,Alice需计算 K A = P 2 + s A Q 2 K_A=P_2+s_AQ_2 K A = P 2 + s A Q 2 E 0 E_0 E 0 K A K_A K A ϕ A \phi_A ϕ A ϕ A ( P 3 ) , ϕ A ( Q 3 ) \phi_A(P_3),\phi_A(Q_3) ϕ A ( P 3 ) , ϕ A ( Q 3 ) ϕ A , ϕ A ( P 3 ) , ϕ A ( Q 3 ) \phi_A,\phi_A(P_3),\phi_A(Q_3) ϕ A , ϕ A ( P 3 ) , ϕ A ( Q 3 )
而Bob则计算 K B = P 3 + s B Q 3 K_B=P_3+s_BQ_3 K B = P 3 + s B Q 3 E 0 E_0 E 0 K B K_B K B ϕ B \phi_B ϕ B ϕ B ( P 2 ) , ϕ B ( Q 2 ) \phi_B(P_2),\phi_B(Q_2) ϕ B ( P 2 ) , ϕ B ( Q 2 ) ϕ B , ϕ B ( P 2 ) , ϕ B ( Q 2 ) \phi_B,\phi_B(P_2),\phi_B(Q_2) ϕ B , ϕ B ( P 2 ) , ϕ B ( Q 2 )
对于共享密钥,Alice计算K S A = ϕ B ( P 2 ) + s A ϕ B ( Q 2 ) K_{SA}=\phi_B(P_2)+s_A\phi_B(Q_2) K S A = ϕ B ( P 2 ) + s A ϕ B ( Q 2 ) E B E_B E B K S A K_{SA} K S A ϕ S A \phi_{SA} ϕ S A K S B = ϕ A ( P 3 ) + s B ϕ A ( Q 3 ) K_{SB}=\phi_A(P_3)+s_B\phi_A(Q_3) K S B = ϕ A ( P 3 ) + s B ϕ A ( Q 3 ) E A E_A E A K S B K_{SB} K S B j ( ϕ S A ) = j ( ϕ S B ) j(\phi_{SA})=j(\phi_{SB}) j ( ϕ S A ) = j ( ϕ S B )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 ea, eb = 110 , 67 p = 2 **ea*3 **eb - 1 F.<i> = GF(p**2 , modulus=[1 ,0 ,1 ]) E0 = EllipticCurve(F, [1 ,0 ]) P2 = E0(118242575052254473701407051403380184157502700009529430046122822477 *i + 57638278144985143549644316704182130279784191379170896458696787312 , 80915735815367072410310689908590367651933218830435520913424043510 *i + 35228327576503752484578273317308597612913304063200715424014549037 ) Q2 = E0(27856673727210297071672501895829918842041821446996051944738115273 *i + 101349537690838191347553037323956940169953967852439843389873653018 , 45955772915614774101614751673022340983778200451506382887743008335 *i + 76499786039494489791183573966490259392789635716963920208794989512 ) P3 = E0(68702305424425607424554396971378391833152415806389206440833676844 *i + 63162905189208938201083385603424075109355856156240516441321158383 , 14452401602439328239712793251073780692192036710425129093829067649 *i + 110903430163815016394569999096524527007769669322432532390635606190 ) Q3 = E0(50967992419888058158544483269655763559879646024537212566396940681 *i + 39165103284419354968504615023980382940222714919046676966425620242 , 113476160032430656302485251779124302915433268423829474022852380544 *i + 74814862075401178218909769629701747112662266906635780085603780902 ) sA = 225902606209514408534212339057054 sB = 38410379124791756271891302485727 def gen_public_key (P2,Q2,P3,Q3,s ): KA = P2+s*Q2 phiA = E0.isogeny(KA,algorithm="factored" ) EA = phiA.codomain() return EA,phiA(P3),phiA(Q3) def gen_shared_secret (EB,pb2,qb2,sA ): KSA = pb2+sA*qb2 phiSA = EB.isogeny(KSA,algorithm="factored" ) return phiSA.codomain().j_invariant() EA,pa3,qa3 = gen_public_key(P2,Q2,P3,Q3,sA) EB,pb2,qb2 = gen_public_key(P3,Q3,P2,Q2,sB) s1 = gen_shared_secret(EB,pb2,qb2,sA) s2 = gen_shared_secret(EA,pa3,qa3,sB) assert s1==s2s1
SIDH在2022年就已经完蛋了XD
在 Castryck-Decru-SageMath 就有对SIDH的攻击方式